Növbəti yazımızda oxuyan.az komandası olaraq sizlərə elmlərin tacı hesab edilən riyaziyyat fənnindən Natural ədədlər bölməsi ilə bağlı ətraflı məlumatlar verməyə və sizlərlə birlikdə nümunə suallar həll etməyə çalışacayıq.
Natural ədədlər deyildikdə nə anlamalıyıq?
Natural ədədlər say sisteminin bir hissəsidir və 1-dən sonsuza qədər bütün müsbət tam ədədləri əhatə edir. Natural ədədlərə sıfır və ya mənfi ədədlər, onluq kəsrlər daxil olmadığı üçün onlara sayma ədədləri də deyilir. Onlar yalnız müsbət tam ədədlər toplusunun daxil olduğu real ədədləri əhatə edir.
Bizlər ətrafımızda hər yerdə cisimləri saymaq üçün (pulları saymaq , günlük hava temperaturunu və vaxtı ölçmək üçün ) rəqəmlərdən istifadə edirik. Cisimləri saymaq üçün istifadə olunan bu rəqəmlərə “natural ədədlər” deyilir. Məsələn, əşyaları sayarkən 5 stəkan, 6 kitab, 1 şüşə və s. kimi ifadələr istifadə edilir.
Natural ədədlər ədədlər çoxluğu kimi də ifadə edilə bilər. Bu zaman ədədlər çoxluğu “N” ilə işarə edilir. Məsələn, N = {1,2,3,4,5,…∞}
Natural ədədlər öz növbəsində iki yerə bölünür:
- Tək natural ədədlər
- Cüt natural ədədlər
Sonu 1, 3, 5, 7 və 9 rəqəmlərindən biri ilə qurtaran natural ədədlərə tək ədədlər, sonu 0, 2, 4, 6 və 8 rəqəmlərindən biri ilə qurtaran natural ədədlərə isə cüt ədədlər deyilir.
Natural ədədlərin ədəd oxunda göstərilməsi
Natural ədədlər ədəd oxundan istifadə edilməklə təqdim oluna bilər. Natural ədədlər mövzusu ilə əlaqədar çoxlu testlər işlədikcə ədəd oxu ilə bağlı suallarla qarşılaşmaq mümkündür. Oxuyan.az platformasında sizlər istənilən mövzuya dair test çalışmalarından yararlana və öz biliklərinizi yoxlaya bilərsiniz.
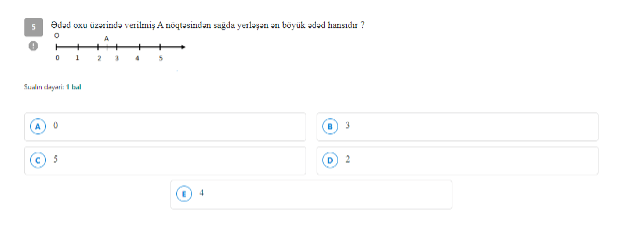
Yuxarıda verilmiş test nümunəsi oxuyan.az platformasında sizlərə təqdim edilən onlarla test nümunələrindən sadəcə biridi. Sualı həll edərkən ilk olaraq sual şərtini diqqətli oxumaq lazımdır. Burada A nöqtəsindən sağda yerləşən ən böyük rəqəmi tapmağımız tələb edilir. A nöqtəsindən sağda yerləşən ədədlər 3, 4 və 5- dir. Bu ədədləri müqayisə edərkən 5 ədədinin daha böyük olduğunu əminliklə deyə bilərik. Məhz bu səbəbdən dolayı, yuxarıda verilmiş sualın cavabı C variantıdır.
Natural ədədin mərtəbələri
Natural ədədlərdə rəqəmlərin tutduğu yer mərtəbə adlanır. Bu mərtəbələr sağdan başlayaraq – təkliklər, onluqlar, yüzlüklər, minliklər onminliklər və.s adlandırılır. Nümunə olaraq şərti verilmiş 5 mərtəbəli olan “abcde” ədədini götürək. Verilmiş ədədi aşağıda mərtəbələr şəklində ifadə edək:
- e – təkliklər mərtəbəsinin vahidlərinin sayı.
- d – onluqlar mərtəbəsinin vahidlərinin sayı.
- c – yüzlüklər mərtəbəsinin vahidlərinin sayı.
- b – minliklər mərtəbəsinin vahidlərinin sayı.
- a – on minliklər mərtəbəsinin vahidlərinin sayı
Mərtəbəlilik anlayışını tam şəkildə anlayan hər bir şagird iki müxtəlif ədədi müqayisə edərkən heç bir çətinlik , çəkməməlidir. Aşağıda sizlər üçün ədədlərin müqayisəsi verilmiş bir başqa test nümunəsi təqdim edəcəyik.
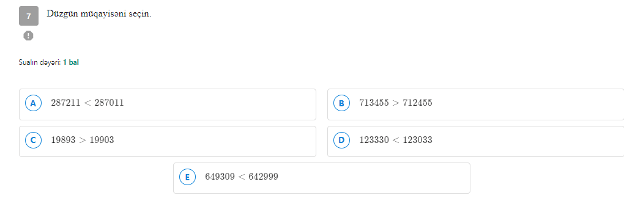
Bu sual nümunəsində doğru cavab B) variantıdır. Bu cür sualları həll edərkən ən böyük mərtəbədən başlayaraq eyni mərtəbələrdə dayanan rəqəmləri bir-bir müqayisə edərək bərabərsizliyi yoxlamaq mümkündür.
Natural ədədlər üzərində əməllər
Natural ədədlər üzərində əməllər aşağıdakı ardıcıllıqla yerinə yetirilir.
- 1.Vurma
- 2.Bölmə
- 3.Toplama
- 4.Çıxma
Əgər mötərizə varsa ilk növbədə mötərizələrin içərisindəki əməllər yerinə yetirilir.
Toplama: Natural ədədlərin toplanmasında iki və daha artıq ədəd iştirak etməlidir.Bu ədədlərə toplananlar alınmış nəticəyə isə cəm deyilir. Nümunə: 540+364=904.Burada 540 və 364 toplananlar 904-isə cəmdir.
Çıxma: Çıxma əməlində də iki ədəd iştirak etməlidir.Misal: 1847-965=882.Burada 1847-azalan, 965-çıxılan, 882-isə fərq adlanır.
Vurma:Natural ədədlərin vurulmasında iştirak edən ədədlərə vuruqlar, alınan nəticəyə isə hasil deyilir.Misal:13*12=156 .Burada 13 və 12 vuruqlar, 156 isə hasildir.
Bölmə:Bölmə əməlində ədədlərdən və : işarəsindən istifadə olunur.Misal:
63:9=7.Burada 63 bölünən 9 bölən 7 isə qismətdir. Ola bilər ki verilmiş ədəd bölənə tam bölünməsin.Məsələn: 87:4=21(qalıq 3) Bu o deməkdir ki, 87-ni 4-ə böləndə 21 alınır qalıq isə 3 olar.Həqiqətən də 21*4+3=87 olar.Bəzən aşağıdakı kimi misallar rast gəlmək olar.
Nümunə 1.
Bölən 12 , qismət 6 , qalıq isə 8-dir.Bölünəni tapın. O zaman qisməti (yəni 6-nı) bölənə (yəni 12-yə) vurub qalığı (yəni 8-i) üstünə gəlirik.Yəni 6*12+8=80
Aşağıdakı düsturları istifadə etməklə bir çox tapşırığı həll etmək mümkündür.
1.Əgər bölünən, qismət və qalıq verilibsə, böləni tapmaq üçün
Bölən=(bölünən-qalıq):qismət
2.Əgər bölən, qismət və qalıq verilibsə, bölünəni tapmaq üçün
Bölünən=bölən*qismət+qalıq
Bölünmə əlamətləri
- Sonu “0” yaxud cüt rəqəmlə qurtaran natural ədədlər 2-yə qalıqsız bölünür.
- Rəqəmləri cəmi 3-ə bölünən natural ədədlər 3-ə qalıqsız bölünür.
- Natural ədədin son iki rəqəmi sıfırdırsa, və ya son iki rəqəminin əmələ gətirdiyi ədəd 4-ə bölünürsə, bu ədəd 4-ə qalıqsız bölünür.
- Sonu “0”- la yaxud “5”-lə qurtaran natural ədədlər 5-ə qalıqsız bölünür.
- Eyni zamanda 2-yə və 3-ə bölünən natural ədədlər 6-ya qalıqsız bölünür.
- Natural ədədin son üç rəqəmi sıfırdırsa, və ya son üç rəqəminin əmələ gətirdiyi ədəd 8-ə bölünürsə, bu ədəd 8-ə qalıqsız bölünür.
- Rəqəmləri cəmi 9-a bölünən natural ədədlər 9-a qalıqsız bölünür.
- Sonu “0”-la qurtaran bütün natural ədədlər 10-a qalıqsız bölünür.
- Eyni zamanda 2-ə və 3-ə bölünən (6-a bölünən) natuarl ədədlər 12-ə bölünür.
- Eyni zamanda 3-ə və 5-ə bölünən ədədlər 15-ə bölünür.
- Son iki rəqəmi 25, 50, 75 və 00 olan ədədlər 25-ə bölünür.
Verilmiş bu əlamətləri nəzərə alaraq aşağıdakı sualı həll etməyə çalışaq.
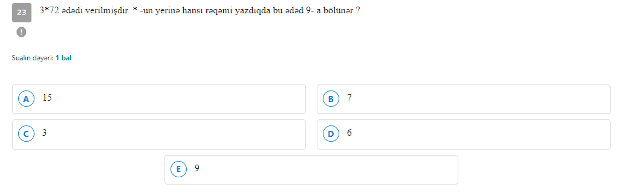
Bu sual nümunəsi 9-a bölünmə əlaməti ilə bağlıdır. Yuxarıda qeyd edildiyi kimi əgər ədədin rəqəmləri cəmi 9-a bölünürsə, bu natural ədəd özü 9-a qalıqsız bölünür. *-un yerində 6 olduğu təqdirdə 3672 ədədi 9-a qalıqsız bölünəcəkdir.
9,483 total views